An Inside Look into Fantom Research’s Formal Model-Driven Development Process

Introduction
Rigorous software development is essential to design safe and secure blockchains. The global cryptocurrency market is valued at over 2 trillion dollars; therefore, the blockchain infrastructure is a lucrative target for hackers who want to exploit system design flaws and implementation bugs.
Unfortunately, the distributed nature of blockchains makes them notoriously difficult to test due to their inherent complexity. The software complexity grows exponentially with each added new node to the network. Thus, new methods of rigorous software development need to be employed for blockchains.
To this end, Fantom is on an exciting new journey to deploy a formal model-driven development process (FMDD), improving the trustworthiness and reliability of our network’s clients and making our network even more reliable. The FMDD approach uses mathematical logic, proofs, and trace-based testing to ensure the network protocol runs correctly. An example of a critical component in modern blockchains is the consensus protocol.
Consensus protocols coordinate processes so that they agree on the state of the blockchain. The consensus protocol is a natural attack vector, notably for double-spending attacks that exploit unsafe protocols and bring them to inconsistent states, where a currency unit can be used twice.
Although all consensus protocols are designed with the intent to be safe, ad-hoc software development makes it difficult to ensure that a complex component such as a consensus protocol is safe for all potential transactions and network configurations, even with best practices in software engineering and testing. Below we outline how our FMDD process works.
Formal System Models
The first step in our FMDD process is describing a component in a formal mathematical language where we can specify precisely what we expect from the component. For this purpose, we use TLA+, a formal language for modeling distributed programs and systems.
The language uses set theory and temporal logic to express program properties. The intention of TLA+ is not to express executable programs like in the Go language; it is there to express an abstraction of a program in the form of a mathematical model and its properties.
For the model, the properties can be either disproven or proven correct with a semi-automatic proof assistant, and/or incorrect instances can be found with a model checker. TLA+ uses a state transition model for describing the execution of a program. The state space may have infinite nature.
For instance, consider a simple consensus protocol. The protocol consists of 3 phases:
- Receiving phase: each validator receives transactions from the network or creates their own and disseminates them.
- Block proposal phase: a block is proposed to be the next block in the blockchain.
- Block decision: after every validator has proposed a block, one of the blocks is decided to be added to the blockchain.
These phases of the protocol are repeated for every generated next block. The critical aspect of the protocol is that only a single block is decided among all validators. Otherwise, the blockchain may result in an inconsistent state that can be manipulated, resulting in double spending attacks. Thus, by formally modeling our protocol, we can ensure that it does not result in inconsistent blocks.
To model our protocol, we view the protocol as a state transition system. Figure 1 below depicts the protocol having four states with transitions between states. Each validator runs through this transition system and produces a block in the “decided block” state while continuing to the next block.
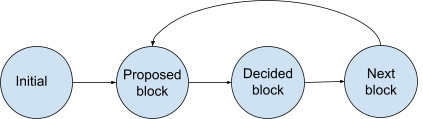
Let’s develop a model in the TLA+ specification reflecting the transitions of our consensus protocol. Our first step is to create a module and define a state in the protocol.
1 ---------- MODULE absconsensus ------------------------------------
2 EXTENDS FiniteSets,
3 Integers,
4 Sequences,
5 TLC
6
7 CONSTANT NumValidators
8
9 Validators == 1..NumValidators
10 -------------------------------------------------------------------
11
12 CONSTANT NumBlocks
13
14 Blocks == 1..NumBlocks
15 -------------------------------------------------------------------
16 VARIABLES
17 phase_label,
18 blocks_to_propose,
19 proposed_blocks,
20 decided_blocks
21 -------------------------------------------------------------------
In lines 1-5, we define a module and import required libraries. Next in lines 7-14, we define two unbound numerical constants NumValidators and NumBlocks along with sets Validators and Blocks derived from these constants. Lastly, we define in lines 16-20 the variables of the system, i.e. variables whose values may change from state to state. The variables:
phase_labelholds the current phase in the consensus in which each validator is.blocks_to_proposeis a function that selects a block for each validator.proposed_blocksis the set of blocks that have been proposed by all validators.decided_blocksthat is a mapping of what block each validator decided on.
After defining the state of the transition system, we define each transition. In TLA+, two transitions need to be specified: Init and Next. From lines 22-26, we define the Init transition which creates an initial state. Here we set all validators to the first phase of the protocol, define our blocks_to_propose function, and initialize the proposed blocks and decided_blocks variables to the empty set and a null mapping, respectively.
22 Init == /\ phase_label = [v \in Validators |-> "receiving"]
23 /\ blocks_to_propose \in [Validators -> Blocks]
24 /\ proposed_blocks = {}
25 /\ decided_blocks = [v \in Validators |-> 0]
26 -------------------------------------------------------------------The Next transition is shown in the snippet below from lines 27-43. We define Next at line 42 as either a Propose action, Decide action, or NextBlock action given for a given validator. Each action has a guard (pre-condition) and an effect, i.e. a change of state. The Propose action defined in lines 27-30 requires that the validator is in the receiving phase. We change its phase to proposed and keep every other validator the same in line 28. We generate a proposed block for the validator in line 29 and add it to the proposed_blocks set and we state that no other variables changed in line 30.
The Decided action similarly has a guard that asserts that no validator is in the receiving phase and that the current validator is in the proposed phase. We then change its phase to proposed and select a decided block in line 31 using the CHOOSE operator to mimic a global random selection.
Lastly, the NextBlock transition simply asserts that all validators have decided and sets the current validator to the receiving phase while resetting the proposed blocks.
27 Propose(v) == /\ phase_label[v] = "receiving"
28 /\ phase_label' = [phase_label EXCEPT ![v] = "proposed"]
29 /\ proposed_blocks' = proposed_blocks \cup {blocks_to_propose[v]}
30 /\ UNCHANGED <<blocks_to_propose, decided_blocks>>
31 GlobalPick(v) == decided_blocks' =
[decided_blocks EXCEPT ![v] = CHOOSE x \in proposed_blocks : TRUE]
31 Decide(v) == /\ ~ \E v1 \in Validators: phase_label[v1] = "receiving"
32 /\ phase_label[v] = "proposed"
33 /\ phase_label' = [phase_label EXCEPT ![v] = "decided"]
34 /\ GlobalPick(v)
35 /\ UNCHANGED <<blocks_to_propose, proposed_blocks>>
36
37 NextBlock == /\ \A v1 \in Validators: phase_label[v1] = "decided"
38 /\ phase_label' = [v \in Validators |-> "receiving"]
39 /\ proposed_blocks' = {}
40 /\ UNCHANGED<<blocks_to_propose, decided_blocks>>
41 -------------------------------------------------------------------
42 Next == \E v \in Validators : Propose(v) \/ Decide(v) \/ NextBlock
43 -------------------------------------------------------------------Recall that the main property we want our consensus property to maintain is consistency. Thus, in line 44 we define a notion of consistency in our specification as: given any two validators have not decided on null (0), i.e. they decided something, then their decisions should be equal. We say that this notion of consistency is a Safety_Invariant in line 45.
44 Consistency == \A v1, v2 \in Validators: decided_blocks[v1] # 0 /\ decided_blocks[v2] # 0 => decided_blocks[v1] = decided_blocks[v2]
45 Safety_Invariant == Consistency
46 ===================================================================Proving Model Correctness
Given we have specified the intended behavior of our system and the properties we desire it to have, we must determine if the model (which is a symbolic state transition system) adheres to these properties at all times. That is for all inputs, configurations, etc.
We achieve this by deriving an inductive invariant. An inductive invariant is a property that holds initially and is preserved after taking any sequence of valid transitions. Let our inductive invariant be inv, the following conditions should hold:
- Init => inv
- inv /\ Next => inv
- inv => Safety_Invariant
Here, rule 1 states that the inductive invariant should hold after initialization. Rule 2 states that the inductive invariant should continue to hold after a transition. Rule 3 states that the inductive invariant implies the correctness property. As is the case with our specification, our correctness property itself is an inductive invariant, i.e. Inv == Consistency so that all three rules trivially hold as shown below:
THEOREM BaseCase == Init => Inv
<1> SUFFICES ASSUME Init
PROVE Inv
OBVIOUS
<1> QED
THEOREM IndCase == Inv /\ [Next]_vars => Inv'
<1> SUFFICES ASSUME Inv /\ [Next]_vars
PROVE Inv'
OBVIOUS
<1> QED
THEOREM PropCase == Inv => Safety_Invariant
OBVIOUSHowever, inductive invariants are often stronger than the safety property and require strengthening by conjoining additional assumptions. The process of finding Inductive invariants is typically manual, semi-automatic using a proof assistant, or fully automatic using an automated reasoning prover.
At Fantom, we have modeled protocols such as DAGRider and CordialMiner with that aforementioned approach using a library approach. With that approach, new DAG-based protocols can be proven with less effort since building blocks can be used for the proof. We have recently made a technical report available.
Correspondence Between TLA+ Model and Implementation
The formal model specifies how the system must behave, and we have proven it adheres to important properties, e.g. consistency. Proving it correct, however, is only half the task. While providing clarity for an implementation, the model itself does not ensure that the implementation will adhere to the specification.
For instance, the implementation may contain various complexities such as communication, buffers, DAGs, and randomness beacons among others. These details may obfuscate whether the implementation adheres to the abstract model. To ensure an approximate correspondence between the implementation and model, we apply several strategies that ensure our implementation adheres to the model with a high degree of certainty.
First, we can statically generate model execution traces using a model checker. These abstract execution traces can be seen as execution paths in our state transitions. They form a basis for tests, as we can map abstract executions to implementation executions.
We instantiate our specification for a finite number of validators, blocks, etc. We then employ the model checkers simulation mode, which given a state, applies a transition to generate the set of possible next states (post-states) and randomly picks a state to continue the process. Consider our consensus protocol example. Since model checkers are bounded, we can generate traces for an instance of our specification.
For example, we can restrict the number of validators to 4 and the number of blocks to generate block ids in {1..4}.
=> Init
phase_label = <<"receiving", "receiving", "receiving", "receiving">>
decided_blocks = <<0, 0, 0, 0>>, …
=> Propose
phase_label = <<"receiving", "receiving", "proposed", "receiving">>
decided_blocks = <<0, 0, 0, 0>>, …
=> Propose
phase_label = <<"proposed", "receiving", "proposed", "receiving">>
decided_blocks = <<0, 0, 0, 0>>, …
=> Propose
phase_label = <<"proposed", "receiving", "proposed", "proposed">>
decided_blocks = <<0, 0, 0, 0>>, …
=> Propose
phase_label = <<"proposed", "proposed", "proposed", "proposed">>
decided_blocks = <<0, 0, 0, 0>>, …
=> Decide
phase_label = <<"proposed", "proposed", "decided", "proposed">>
decided_blocks = <<0, 0, 1, 0>>, …This can then be converted into a test case to check that our implementation’s execution adheres to this trace.
Second, we apply a complementary approach where we generate traces from the implementation using fuzzing and simulators and check that the software trace is a behavior of the proven model. We instrument the implementation to log procedures that correspond to actions in the model and instrument the state change after each procedure. We then convert this trace into TLA+ logic constraints (trace model), and using a model checker, check that for a state and an action. The set of possible states (post-condition) contains the state in the trace.
Simulator
Testing various scenarios that occur in traces of our model is difficult in a real-world distributed environment because external parameters cannot be controlled. Therefore, before integrating our software into the client software, we isolate it and test its behavior in a simulation.
This allows us to directly control various aspects of not only the consensus protocol but also external aspects, e.g. network latency, crashes, etc. After we have enough guarantee that the component behaves correctly for various scenarios, we can port the component into the client.
Putting It All Together
Overall, the FMDD process is depicted below:
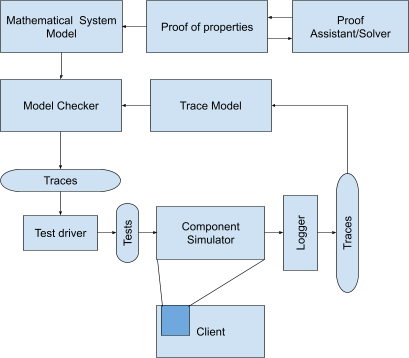
By leveraging a formal model, we are able to ensure software reliability and provide a source of truth to developers with much more precision than ad-hoc documentation. The formal modeling process is not a time liability as it forces engineers to think ahead of time about the consequences of design decisions as well as to align all stakeholders on the design.
Overall we believe that applying formal methods results in a long-term net gain.
Conclusion
While the performance of a blockchain is quick to make headlines, impressive performance numbers are all in vain on an incorrect blockchain. Moreover, once a client is deployed, patching clients on all nodes is difficult, particularly in public blockchains.
At Fantom, we argue that our FMDD approach, while adding some overhead to development, ensures that we are building the right component and that it does not hit unexpected corner cases when deployed.



